手書き数字を認識する機械学習

数字を認識するように学習する小さなニューラルネットワーク
入力レイヤー、出力レイヤー、および活性化関数によってどのように単一のニューロンがモデル化されるかについて、前回で説明しました。活性化関数は入力を取り、与えられた重みと組み合わせて出力を計算します。手書き数字認識ネットワークに注目する前に、シンプルなニューラルネットワークがその出力をどのように計算するかを見てみましょう。
ニューラルネットワークの出力とその計算方法
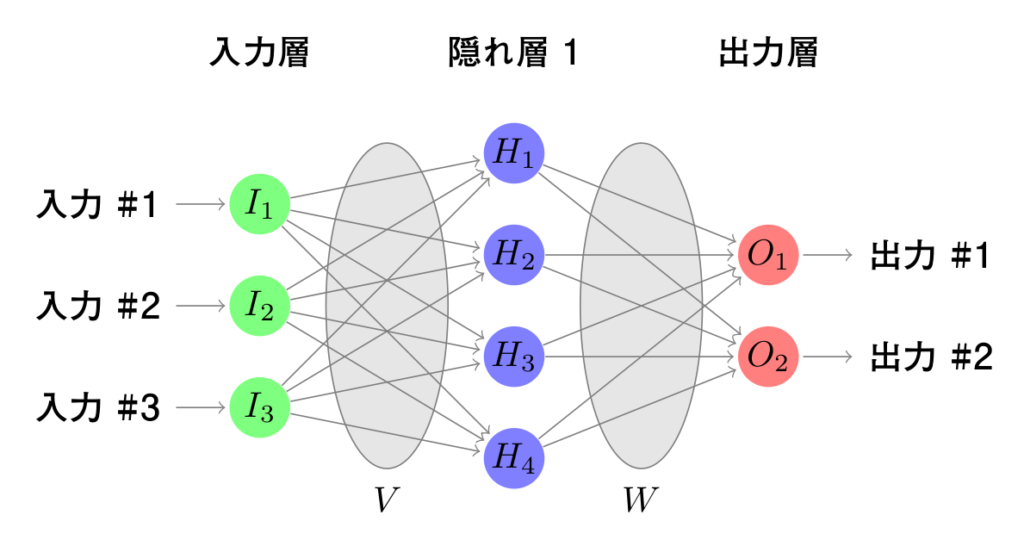
V(入力層と隠れ層の間)とW(隠れ層と出力層の間)は、接続の重みと仮定します。この場合にはV1,3はI1とH3との間の接続の重みを表します。
ネットワークの出力を計算するために、入力値から始めて、隠れ層の値を計算します。
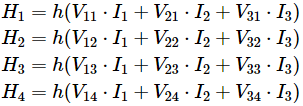
hはある指標関数です。
次に、出力ニューロンを計算します。
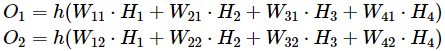
数学では、通常、上記を記述するために行列/ベクトルの乗算を使用します。
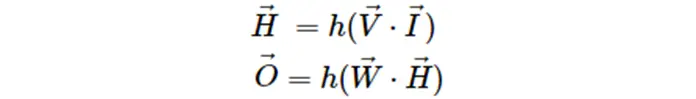
ニューラルネットワークの出力を計算することができたので、その結果を使って学習させます。入力値と出力値のセットがあり、ニューラルネットワークに合わせて重みを調整します。各入力データに対して出力を計算し、計算結果と期待される出力を比較したその差を損失といいます。重みを調整することにより、この損失を最小限に抑えようとします。
手書き数字を訓練する例

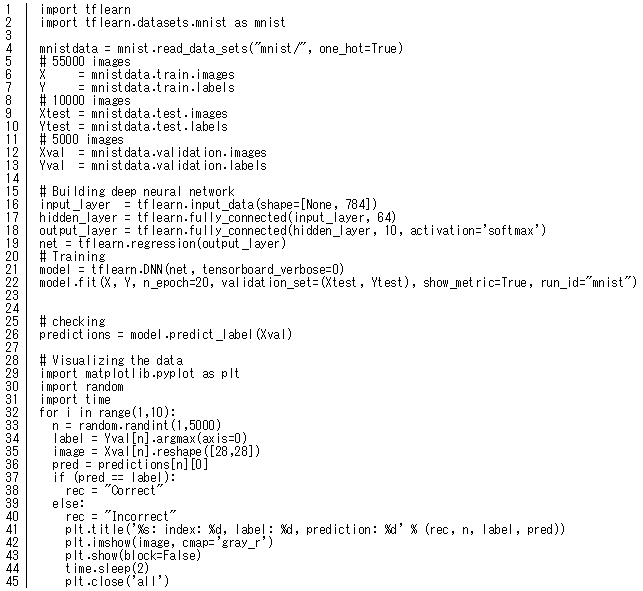
下記のコードはTFLearnというフレームワークを使ってPythonで書かれています。TFLearnはGoogleのTensorFlowに実装されています。TFLearnとTensorFlowをインストールした場合は、下記のコードをそのまま起動できます。
(コードのダウンロードはこちら)
コードの説明
l1:tflearnフレームワークをインポートし、テンソルフローを読み込み
l2:mnistデータセット関数をインポート
l4:MNISTデータをロードし、トレーニングセットとテストセットに分割
l5-l13:学習データ、テストデータ、バリデーションデータを設定
l15-22:ニューラルネットワークを構築
l16:入力層を784個のニューロンで定義
l17:完全に接続された64個のニューロンの隠れ層
l18:出力層は10個のニューロンで構成され、10個の値の和が1になる確率を保証する特別なアクティブ化関数 `softmax 'を使用
l19:どのように重みを学習するか、ネットワークを定義
l21:モデル(深いニューラルネットワークDNN (Deep Neural Network))を作成
l22:訓練セットXとYに適合し、検証セットtestXとtestYに対するテスト
l26:Xvalに対して認識の結果を計算
l28-45:ランダムの画像を10枚を表示
ニューラルネットワークのテスト
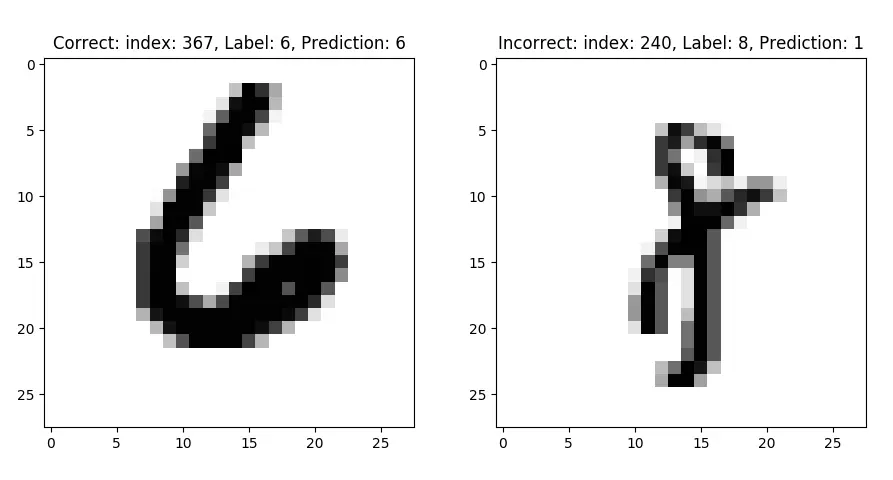
下図の場合、左側は画像の上部に「Correct: index:367,Label:6,Prediction:6」という結果が表示されている通り、「正解: 367枚目の画像,正解:6,予測:6」となり、予測は正解です。
右側は「Incorrect: index:240,Label:8,Prediction:1」と表示されている通り、「不正解: 240枚目の画像,正解:8,予測:1」となり予測は不正解となりました。見た目には8に見えますが、予測した値が「1」となったためです。
上記のシンプルなコードでだいたい92%の認識率になりますが、例のとおり不正解もあります。
■関連ページ
【アクセリアのサービス一覧】
・サービスNAVI
サービスにご興味をお持ちの方は
お気軽にお問い合わせください。
Webからお問い合わせ
お問い合わせお電話からお問い合わせ
平日09:30 〜 18:00
Free Service










