Specification and Verification of Software with CafeOBJ - Part 2 - Basics of CafeOBJ

This blog continues Part 1 of our series on software specification and verification with CafeOBJ.(Part 1)

CafeOBJ can be obtained from the website cafeobj.org. The site provides binary packages built from Linux, MacOS, and Windows, as well as the source code for those who want to build the interpreter themselves. Other services provided are tutorial pages, all kind of documentation (reference manual, wiki, user manual).

What is CafeOBJ

Let us recall some of the items mentioned in the previous blog. CafeOBJ is an algebraic specification language, as well as a verification and programming language. This means, that specifications written in CafeOBJ can be verified right within the system without the need to regress to external utilities.

As algebraic specification language it is built upon the logical foundation formed by the following items: (i) order sorted algebras, (ii) co-algebras (or hidden algebras), and (iii) rewriting logic. As verification and programming language it provides the user with an executable semantics of the equational theory, a rewrite engine that supports conditional, order-sorted, AC (associative and commutative) rewriting, a sofisticated module system including parametrization and inheritance, and last but not least a completely free syntax.

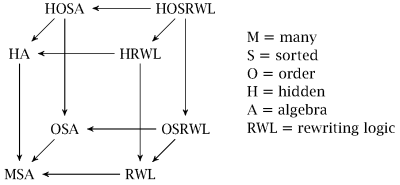
The algebraic semantics can be represented by the CafeOBJ cube exhibiting the various extensions starting more many sorted algebras:
For the algebraically inclined audience we just mention that all the systems and morphisms are formalized as institutions and institution morphisms.Let us now go through some the the logical foundations of CafeOBJ:

Term rewriting is concerned with systems of rules to replace certain parts of an expression with another expression. A very simple example of a rewrite system is:

　append(nil, ys) → ys
　append(x : xs, ys) → x : append(xs, ys)

Here the first rule says that you can rewrite an expression append(nil, ys) where ys can be any list, with ys itself. And the second rule states how to rewrite an expression when the first element is not the empty list.

A typical reduction sequence - that is application of these rules - would be:

append(1 ∶ 2 ∶ 3 ∶ nil, 4 ∶ 5 ∶ nil) → 1 ∶ append(2 ∶ 3 ∶ nil, 4 ∶ 5 ∶ nil)
　　　　　　　　　　　　　　　　　　 → 1 ∶ 2 ∶ append(3 ∶ nil, 4 ∶ 5 ∶ nil)
　　　　　　　　　　　　　　　　　　 → 1 ∶ 2 ∶ 3 ∶ append(nil, 4 ∶ 5 ∶ nil)
　　　　　　　　　　　　　　　　　　 → 1 ∶ 2 ∶ 3 ∶ 4 ∶ 5 ∶ nil

Term rewriting is used in two different ways in CafeOBJ: First as execution engine that considers equations as directed rules and uses them to reduce expressions. And at the same time rewriting logic is included into the language specification allowing for reasoning about transitions.

Most algebras we learn in school or even at the university are single sorted, that is all objects in the algebra are of the same type (e.g., integers, reals, function space). In this case an operation is determined by its arity, that is the number of arguments.

In the many sorted and order sorted case the simple number of arguments of a function is not enough, we need to know for each argument its type and also the type of the value the function returns. Thus, we assume a signature (S,F) given, such that S is a set of sorts, or simply sort names, and F is a set of operations f: s1, s2, ..., sk → s where all the s are sorts.

As an example assume we have two sorts, String and Int, one possible function would be

　substr: String, Int, Int → String

which would tell us that the function substr takes three arguments, the first of sort String, the others of sort Int, and it returns again a value of sort String.

In case the sorts are (partially ordered), we call the corresponding algebra order sorted algebra.

Using order sorted algebras has several advantages compared to other algebraic systems:

　・polymorphism (parametric, subsort) and overloading are natural consequences of ordered sorts;
　・error definition and handling via subsorts;
　・multiple inheritance;
　・rigorous model-theoretic semantics based on institutions;
　・operational semantics that executes equations as rewrite rules (executable specifications).

We want to close this blog post with a short history of CafeOBJ and a short sample list of specifications that have been carried out with CafeOBJ.

CafeOBJ, as an algebraic specification language based on equational theory, has its roots in CLEAR (Burgstall and Goguen, early 70s) and the OBJ language (Goguen et al, 70-80s SRI and UCI San Diego). The successor OBJ2 was developed by Futatsugi, Goguen, Jouannaud, and Meseguer at UCI San Diego in 1984, based on Horn logic, sub-sorts, and parametrized modules.

The developer then moved on to different languages or extensions: Meseguer started to develop Maude, Jouannaud moved on to develop Coq, an unrelated language, and Futatsugi built upon the OBJ3 language by Kirchner et al to create CafeOBJ.

Example specifications carried out in CafeOBJ are authentication protocols (NSLPK, STS, Otway-Rees), key secrecy PACE protocol (German passport), e-commerce protocols (SET), real time algorithms (Fischer’s mutual exclusion protocol), UML semantics, formal fault tree analysis.

---

In the next blog post we will make first steps with the CafeOBJ interpreter and see how to define modules, the basic building blocks, and carry out simple computations.


■関連ページ
【アクセリアのサービス一覧】
　・サービスNAVI